ДВИЖЕНИЕ ТЕЛА С ПЕРЕМЕННОЙ МАССОЙ: ВЗЛЕТ РАКЕТЫ
Рассмотрим указанную задачу в максимально упрощенной постановке. Наши цели:
а) достичь качественного понимания того, как скорость ракеты меняется во время взлета, как влияют на полет разные факторы;
б) оценить оптимальное соотношение параметров, при котором ракета достигнет первой космической скорости и сможет вывести на орбиту полезный груз.
Таким образом, обсуждаемая модель имеет черты как дескриптивной, так и оптимизационной.
Взлет ракеты - сложный процесс, который неизбежно следует огрубить в попытке получения относительно простых и качественно верных результатов. Например, примем, что сила тяги двигателя - величина постоянная на всем этапе разгона. Реально это, скорее всего, не так. но при упрощенном анализе колебаниями силы тяги пренебрежем, равно как и влиянием случайных порывов ветра и множеством других случайных и неслучайных факторов. Но при таком, даже самом упрощенном, анализе нельзя пренебречь наличием сопротивления воздуха, которое при высоких скоростях очень велико. Ни в коем случае нельзя пренебречь и убыванием массы ракеты в процессе взлета - оно огромно и составляет большую часть исходной массы. Так, у одной из крупнейших отечественных ракет «Энергия» стартовая масса составляет 20000 тонн, а к концу взлета всего 200 тонн.
Поиск математического описания проблем не составляет - в его основе все тот же второй закон Ньютона. Поскольку ракета очень быстро набирает столь высокую скорость, что линейной составляющей силы сопротивления заведомо можно пренебречь, то Fconp = k2v2. Примем, что топливо расходуется равномерно вплоть до его полного выгорания, т.е.

где m0 - начальная масса ракеты, ткон - конечная (т.е. масса полезного груза, выводимого на орбиту), ? - расход топлива; это допущение согласуется с допущением о постоянной силе тяги. Уравнение движения принимает вид в проекции на вертикальную ось
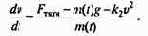
Казалось бы, можно задаться некоторыми значениями величин Fтяги, т0, ?, k2 и проводить моделирование, но это была бы чисто формальная деятельность, не учитывающая еще одного важнейшего обстоятельства.
Поскольку ракета взлетает на огромную высоту (сотни километров), ясно, что сила сопротивления в менее плотных слоях атмосферы не может быть такой же, как вблизи поверхности Земли (при равных скоростях). Действительно, в коэффициент k2
входит величина r -плотность окружающей среды, которая на «космических» высотах во много раз меньше, чем вблизи поверхности. Заглянем в справочник: на высоте 5,5 км плотность воздуха вдвое меньше, чем у поверхности, на высоте 11
км - вчетверо и т.д. Математически зависимость плотности атмосферы от высоты хорошо передается формулой
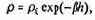
где b = 1,29•10-4
(h измеряется в метрах, ?0 - плотность вблизи поверхности Земли). Поскольку величина h
меняется в ходе полета, уравнение для изменения h(t) следует добавить к уравнению (7.17) и записать следующую систему дифференциальных уравнений:
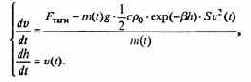
Наша модель становится все более реалистической. Ее совершенствование можно продолжить - например, учесть наличие у ракеты нескольких ступеней, каждая из которых имеет свой запас топлива и тягу двигателя - считая, что после уменьшения массы до некоторого значения сила тяги скачком изменяется; оставим это для самостоятельных размышлений. Перед решением уравнений удобно обезразмерить переменные. Естественной характерной скоростью в данной задаче является первая космическая скорость v* ? 7,8 км/с, при которой возможен вывод на орбиту полезного груза; характерное время - момент полной выработки горючего
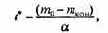
где mкон - масса груза. Реально t* - две-три минуты. За характерную высоту можно взять, например, h* - ту, на которой плотность атмосферы уменьшается в 10 раз (примерно 17 км). Последняя величина может показаться несколько произвольной (впрочем, она таковой и является), но все равно удобнее измерять расстояния в данной задаче относительно величины, равной нескольким километрам, чем в метрах в системе СИ. Итак, введя безразмерные переменные

после несложных преобразований получим уравнения
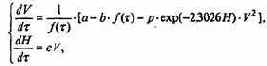
где f(?) - известная функция:
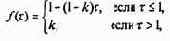
а безразмерные параметры a, b, p, e, k выражаются через исходные так:
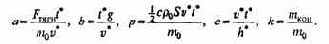
То, что f(?) определяется двумя формулами, связано с наличием двух этапов полета: до и после выработки топлива. Безразмерное время, разделяющее эти этапы - ? = 1; если к этому моменту безразмерная скорость V ? 1, то первая космическая скорость достигнута, в противном случае - нет. Параметр а
управляет режимом полета; если при достижении величиной V значения, равного единице, топливо еще не все выработано (т.е. ? < 1), можно с этого момента либо положить а = 0 («выключить двигатель»), либо продолжать разгон - в зависимости от постановки задачи. Рис. 7.13 иллюстрирует влияние изменения параметра о на динамику взлета ракеты в рамках принятых выше предположений при фиксированных значениях остальных параметров.
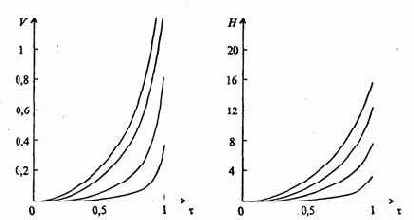
Рис. 7.13. Зависимости V(?) и H(?) при а =
0,2, a = 0,3, a = 0,4 и а = 0,5
(кривые на рисунках слева направо)
